【线性代数】最小二乘与投影矩阵

​ 前一篇文章《正交投影》中我们讲述了正交投影，现在我们来从正交投影的角度来看看我们熟悉的最小二乘法。我记得最早知道最小二乘法是在大一上高数课的时候，我们首先回顾一下什么是最小二乘法。

---

最小二乘法

最近机器学习比较火，机器学习中的许多算法都是对信息进行分类，比如说支持向量机就是根据已知信息来分类，神经网络可以找到输入输出的关系（当然，不能给出具体的数学表达式），这两种算法都能找到输入与输出的关系，分类和回归总是相辅相成的。以后有时间也准备写写关于机器学习方面的算法（现在终于开始写了图解例说机器学习系列—2020.0831）。 言归正传，最小二乘法的作用也是从一组数据中找到输入与输出之间的关系。

原理：

设经验方程是$y=f(x)$，方程中含有一些待定系数$a_n$，给出真实值${(x_i,y_i)|i=1,2,\cdots,n}$,将这些$x, y$值代入方程然后作差，可以描述误差：$y_i-f(x_i)$，为了考虑整体的误差，可以取平方和，之所以要平方是考虑到误差可正可负直接相加可以相互抵消，所以记误差(注意误差函数的选择有很多种，我们选用典型的误差函数)为：

$$E=\sum\limits_{i=1}^n(y_i-f(x_i))^2$$

它是一个多元函数，有$a_n$共$n$个未知量，现在要求的是最小值。所以必然满足对各变量的偏导等于$0$，于是得到$n$个方程：

$$\begin{aligned} \left\{ \begin{array}{**lr**} \frac{\partial E}{\partial a_1}=0\\ \frac{\partial E}{\partial a_2}=0\\ \quad\quad\vdots\\ \frac{\partial E}{\partial a_n}=0 \end{array} \right. \end{aligned}$$

$n$个方程确定$n$个未知量为常量是理论上可以解出来的。用这种误差分析的方法进行回归方程的方法就是最小二乘法。

---

最小二乘与投影

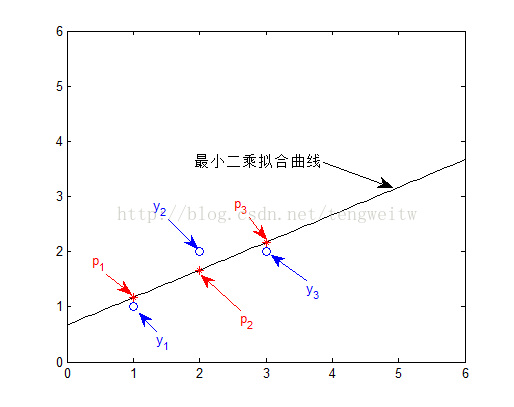
我这个人不喜欢看这些理论，公式推导，而更喜欢用例子来展示算法的思想。例如，在二维坐标系中，有三点，$(1, 1), (2, 2), (3, 2)$，那如何用一条直线来拟合这些点呢？

首先，我们可以假设直线表达式如下所示：

$$a_1x+a_2=y$$

然后计算误差函数：

$$\begin{aligned} E&=(a_1+a_2-1)^2+(2a_1+a_2-2)^2+(3a_1+a_2-2)^2\\ &=14a_1^2+3a_2^2+12a_1a_2-22a_1-10a_2+9 \end{aligned}$$

在求得误差函数$E$对系数$a,b$的偏导，并使之为$0$：

$$\frac{\partial E}{\partial a_1}=28a_1+12a_2-22=0\\ \frac{\partial E}{\partial a_2}=6a_2+12a_1-10=0$$

由上式得到系数$a,b$的值，并得到拟合直线表达式：

$$a_1=\frac{1}{2},a_2=\frac{2}{3}\rightarrow y=\frac{1}{2}x+\frac{2}{3}$$

通过最小二乘法得到的曲线如下：

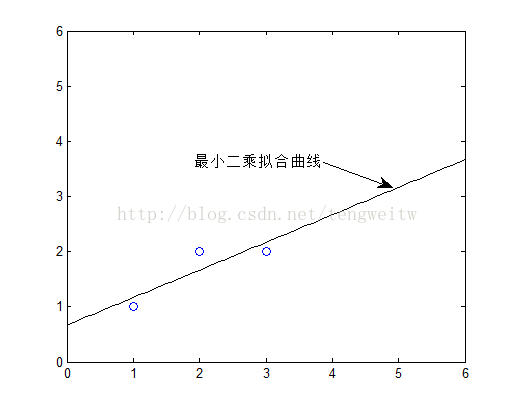
线性代数角度看最小二乘法：

同样假设拟合直线的表达式设为：

$$a_1x+a_2=y$$

拟合的目的就是使得数据点都满足上述函数表达式，即：

$$a_1+a_2=1\\ 2a_1+a_2=2\\ 3a_1+a_2=2$$

用矩阵形式表示如下：

$$\begin{aligned} \underbrace{\left[\begin{array}{cc}1&1\\2&1\\3&1\end{array}\right]}_{A} \underbrace{\left[\begin{array}{c}a_1\\a_2\end{array}\right]}_{a} =\underbrace{\left[\begin{array}{c}1\\2\\2\end{array}\right]}_{b} \end{aligned}$$

上面的式子通过高斯消元后，可以发现是无解的！

​ 我们可以发现等式的左边$Aa$的值是矩阵$A$中各个列向量的线性组合，若$Aa=b$有解的话，则$b$一定在矩阵$A$的列空间内。上面的例子中，右边的向量显然不在其列空间中，因此方程无解。最小二乘法的思想就是在矩阵$A$的列空间中找到一个向量$p$，使得$p$与$b$的误差最小。下面我们就来求$b$:

$$b=\left[\begin{array}{c}1\\2\\2\end{array}\right], p=\left[\begin{array}{c}p_1\\p_2\\p_3\end{array}\right], e=b-p, E=\Vert e\Vert^2, Aa=p$$

$Aa=p$是肯定有解的，因为$p$在矩阵$A$的列空间中。要使得$e$向量的长度最短，当且仅当$p$为$b$在矩阵列空间上的投影！有上一篇《正交投影》中投影矩阵的通式可得：

$$p=Pb=A(A^TA)^{-1}A^{T}b$$

那么将$p$代入公式$Aa=p$可得：

$$Aa=p=A(A^TA)^{-1}A^Tb\rightarrow A^TAa=A^Tb$$

将具体数值代入得：

$$A^TA=\left[\begin{array}{ccc}1&2&3\\1&1&1\end{array}\right] \left[\begin{array}{cc}1&1\\2&1\\3&1\end{array}\right]= \left[\begin{array}{cc}14&6\\6&3\end{array}\right]\\ A^Tb=\left[\begin{array}{ccc}1&2&3\\1&1&1\end{array}\right] \left[\begin{array}{c}1\\2\\2\end{array}\right]= \left[\begin{array}{c}11\\5\end{array}\right]$$

则可以得到：

$$\left[\begin{array}{cc}14&6\\6&3\end{array}\right] \left[\begin{array}{c}a_1\\a_2\end{array}\right] =\left[\begin{array}{c}11\\5\end{array}\right]\rightarrow \begin{aligned} \left\{ \begin{array}{**lr**} 14a_1+6a_2=11\\ 6a_1+3a_2=5 \end{array} \right. \end{aligned}\\ \rightarrow a_1=\frac{1}{2},a_2=\frac{2}{3}\rightarrow y=\frac{1}{2}x+\frac{2}{3}$$

$b, p, e$向量分别可以表示如下：

$$\begin{aligned} \underbrace{\left[\begin{array}{c}1\\2\\2\end{array}\right]}_{b}= \underbrace{\left[\begin{array}{c}\frac{6}{7}\\\frac{10}{6}\\\frac{13}{6}\end{array}\right]}_{p} +\underbrace{\left[\begin{array}{c}-\frac{1}{6}\\\frac{2}{6}\\-\frac{1}{6}\end{array}\right]}_{e} \end{aligned}$$

$p, b$在图中的表示如下：